Gravità Analoga

Buchi neri in laboratorio.

(A cura di Alberto Canali, Università di Trento)

Una delle più grandi sfide della fisica moderna è quella di osservare direttamente i buchi neri, sia per poter avere delle evidenze sperimentali della loro esistenza, oltre che per trarre delle considerazioni sperimentali con cui confrontare le teorie. Fino a quest’anno le uniche osservazioni fatte erano di tipo indiretto: ad esempio osservando l’effetto gravitazionale di un buco nero sulle stelle vicine o studiando sorgenti di raggi X nello spazio. Solo grazie agli studi dell’Event Horizon Telescope si è riusciti finalmente ad ottenere la prima, incredibile, fotografia dell’orizzonte degli eventi di un buco nero, la superficie oltre la quale nemmeno la luce può fuggire. Ciononostante la realizzazione di osservazioni sperimentali dirette di fenomeni fisici che avvengono sull’orizzonte non è ancora possibile.

La prima foto di un buco nero scattata dall’Event Horizon Telescope (The EHT Collaboration, “First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole.”, Astrophys. J. 875 (2019) no.1, L1).

Per testare le teorie, come ad esempio la radiazione di Hawking o la Superradianza, servono altri banchi di prova, più comodi e facili da manipolare, i sistemi analoghi, degli apparati fisici che presentano alcune caratteristiche simili a quelle dei buchi neri. Tuttavia che lavorano con un numero inferiore di dimensioni: invece delle 3 + 1 dello spazio tempo si usa una dimensione spaziale per “simulare” lo scorrere del tempo. La prima teorizzazione dei modelli analoghi è attribuita a W. H. Unruh che ipotizzò, nel 1981, la possibilità di osservare un analogo nel contesto di onde sonore che si propagano in un mezzo in movimento. Questi analoghi possono essere realizzati in diversi campi: utilizzando condensati di Bose-Einstein, sistemi di ottica non lineare, suono e acqua.

Buchi Neri: concetti base

Un buco nero è una soluzione particolare, detta “di vuoto”, delle equazioni di Einstein: il caso più semplice è quello di Schwarzschild ossia la soluzione ottenuta considerando un sistema (con massa $M$) statico e a simmetria sferica. Trovare una soluzione delle equazioni di Einstein vuol dire poter scrivere la metrica del sistema, che in questo caso è quella di Schwarzschild.

Metrica di Schwarzschild

Descrive il modo in cui la geometria dello spazio tempo viene modificata dalla presenza della massa del buco nero, che risulta essere l'unico parametro significativo del problema. La metrica di Schwarzschild è: $$ ds^2 = -\left( 1 - \frac{2M}{r} \right) dt^2 + \left( 1 - \frac{2M}{r} \right)^{-1}dr^2 + r^2 d\Omega^2 $$ il primo termine descrive come è modificata la componente temporale dello spazio-tempo, la seconda come è modificata la componente radiale (la metrica è scritta in coordinate sferiche per la parte spaziale) e l'ultimo termine descrivere entrambe le componenti angolari, che data la simmetria sferica non dipendono dall'unico parametro del problema.

La metrica in coordinate sferiche presenta due singolarità: una a $r = 2M = r_S$ (detto raggio di Schwarzschild) e una a $r = 0$. Si può vedere come la prima singolarità sia in realtà non fisica, ma solo un problema della scelta di coordinate e sia quindi eliminabile (ossia usando altre coordinate possiamo ottenere una metrica che non presenti problemi a $r_S$). La singolarità a $r = 0$ è invece una singolarità fisica non eliminabile e non è tutt’oggi ancora ben chiaro cosa succeda al centro di un buco nero.

Il raggio di Schwarzschild identifica una superficie nello spaziotempo sulla quale la velocità di fuga dall’attrazione gravitazionale del buco nero è pari a $c$, la velocità della luce: questo è il nostro orizzonte degli eventi. Dunque qualunque informazione è persa per sempre, ma è del tutto vero? Un buco nero è interamente nero? Spoiler: no. Infatti questi corpi emettono comunque della radiazione, ma prima di introdurre questo concetto vale la pena affrontare un’altra specie di buco nero, leggermente diversa (e meno semplice) di quella appena affrontata.

I Buchi neri di Kerr sono buchi neri che ruotano attorno ad un asse con una certa velocità. Questa classe di buchi neri non è caratterizzata unicamente dalla massa $M$, ma anche dal momento angolare $J$.

Metrica di Kerr

Definendo il parametro $a = \dfrac{J}{M}$, la metrica che descrive i buchi neri di Kerr è la seguente: $$ \begin{split} ds^2 = & - \frac{\Delta - a^2 \sin^2 \theta}{\rho^2}dt^2 - 2 a^2 \frac{2 M r \sin^2 \theta}{\rho^2} dt d\varphi + \\ & + \frac{(r^2 + a^2)^2 - a^2 \Delta \sin \theta^2}{\rho^2} \sin^2 \theta d\varphi^2 + \frac{\rho^2}{\Delta} dr^2 + \rho^2d \theta^2 \end{split} $$ dove sono state introdotte le due quantità $\Delta = r^2 - 2 M r + a^2$ e $\rho^2 = r^2 + a^2 \cos^2 \theta$. Si noti che ponendo $a = 0$ ritroviamo la soluzione di Schwarzschild.

Questa configurazione non ha simmetria sferica, ma assiale rispetto all’asse di rotazione del buco nero. La differenza principale rispetto alla metrica precedente è la presenza di un termine misto di componente angolare e temporale: questo mixing dà origine a un nuovo fenomeno molto interessante. La rotazione del buco nero fa sì che intorno ad esso, al di fuori dall’orizzonte degli eventi, vi sia una regione di spazio in cui niente è in grado di rimanere fermo ed è costretto a co-rotare con il buco nero, pur potendo comunque allontanarsi da esso: questa regione è chiamata ergoregione.

Ricostruzione al computer, tramite ray tracing, di come un buco nero di Kerr modifichi lo spazio tempo attorno a sé.

Con queste basi possiamo provare a introdurre brevemente alcuni fenomeni particolari che avvengono in presenza di un buco nero: la radiazione di Hawking e la superradianza.

Radiazione di Hawking

La radiazione di Hawking è un processo per cui un buco nero emette particelle a una certa energia, ed è un fenomeno che emerge quando si cerca di studiare un buco nero facendo uso di teoria quantistica dei campi. Su scale di tempo molto ridotte, in accordo con il principio di indeterminazione $\Delta E \Delta t > \frac{1}{2} \hbar$, coppie di particelle e antiparticelle si creino e annichiliscano continuamente. Se questo succede in prossimità dell’orizzonte degli eventi è possibile che una delle due particelle cada dentro il buco nero, rimanendo intrappolata per sempre, lasciando l’altra libera di scappare lontano. Nel suo modello Hawking interpretò l’emissione, costante, di queste particelle come l’emissione di un corpo nero perfetto a una certa temperatura, detta di Hawking, inversamente proporzionale alla massa del buco nero: $T_H = \dfrac{\hbar}{8 \pi M}$. Dato che i buchi neri sono molto massivi (i più leggeri possono essere dell’ordine di 3 masse solari fino ad arrivare a diversi milioni), la temperatura è di gran lunga inferiore alla temperatura di 2.7 K del fondo cosmico ($T_H = 6.170 \times 10^{-8} \text{K} (\frac{M_\odot}{M}$)), dunque impossibili da osservare.

Mentre la radiazione di Hawking è un fenomeno che coinvolge entrambe le specie di buchi neri, la superradianza è tipica dei buchi neri di Kerr, ossia di quelli rotanti. Di base è un fenomeno meno complesso, in quanto non coinvolge teoria dei campi, ma è basato sul principio di conservazione dell’energia. Quando, rispettando certe condizioni, un’onda esterna interagisce con il buco nero rotante, essa è in grado di “rubare” energia rotazionale al buco nero, che dunque rallenta, e proseguire la sua strada con un’ampiezza aumentata, avendo incrementato la sua energia.

Come creare un orizzonte analogo

Abbiamo detto che la caratteristica fondamentale di un buco nero è la presenza di un orizzonte degli eventi, che demarca le regioni in cui la velocità di fuga è superiore (all’interno) o inferiore (all’esterno) a c. L’idea di base è dunque quella di creare un sistema che presenti una proprietà simile, un così detto orizzonte analogo. Per realizzarlo dobbiamo creare un sistema che presenti una velocità di fuga non costante nello spazio, così che ciò che si propaga sopra di esso, ad esempio delle onde, superato un certo punto rimanga intrappolato (come mostrato in figura 3). In altre parole facciamo in modo di avere una zona subluminale (con velocità di fuga minore di ciò che si muove sopra di esso) e una zona superluminale (con velocità di fuga troppo grande).

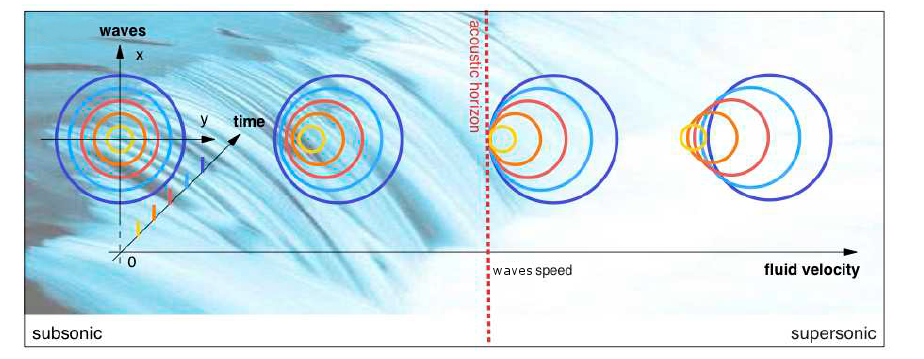
Quando la velocità delle onde (linea tratteggiata di rosso) è uguale alla velocità del fluido abbiamo la creazione dell’orizzonte analogo (C. Barceló, S. Liberati, M. Visser, “Analogue Gravity”, Living Rev. Rel. 14 (2011) 3)

Tra i diversi modi con cui possiamo realizzare l’orizzonte analogo prendiamo in considerazione un caso puramente classico. Studiamo infatti un sistema composto da una vasca d’acqua, in cui abbiamo un flusso di background con velocità variabile e delle perturbazioni, cioè delle onde, che si muovono a velocità costante.

Se trattiamo le onde come piccole perturbazioni, possiamo associare ai campi di velocità del flusso di background e delle onde stesse un potenziale scalare che soddisfa l’equazione di Bernoulli. Alla fine di tutto le perturbazioni sono governate da un’equazione delle onde che può essere riscritta utilizzando il formalismo della relatività come l’equazione di Klein-Gordon (equazione delle onde nello spazio-tempo, 3 + 1 dimensionale): nei sistemi analoghi operiamo in uno spazio 2 + 1 dimensionale. L’equazione riscritta in formalismo quadridimensionale è:

$\Box \delta \Phi_0 = \frac{1}{\sqrt {-g}} \partial_\mu (\sqrt {-g} g^{\mu\nu}\partial_\nu \delta \Phi_0) = 0$,

dove il $\Box$ è il laplaciano al quadrato e $g^{\mu\nu}$ è la metrica effettiva del sistema. Scritta in forma matriciale:

\[g_{\mu\nu}^{\text {eff}} = \frac{1}{gh_B} \begin{pmatrix} gh_B - v_B^{\parallel\ 2} & {v_B^x} & - {v_B^y}\\{v_B^x} & - {1} & 0 \\- {v_B^y} & 0 & - {1} \end{pmatrix}\]

Possiamo osservare che il primo elemento della matrice ha la forma desiderata per la creazione dell’orizzonte analogo: quando il primo termine della metrica si annulla, le onde non possono più superare questo punto, rimanendo intrappolate all’interno del buco nero sonico.

Realizzazione sperimentale

Vediamo ora rapidamente come viene implementato un esperimento di gravità analoga. In laboratorio questo viene realizzato usando una vasca piena di acqua a profondità variabile e uno scarico che crea un vortice per simulare un buco nero rotante. In figura 4 è riportato il setup dell’Università di Nottingham nel “Quantum Gravity Laboratory” volto a osservare un effetto di superradianza.

Per poter utilizzare la trattazione precedente (regime delle piccole oscillazioni), occorre che le onde abbiano perturbazioni verticali molto minori rispetto all’altezza della vasca, a sua volta di dimensioni piccole confrontate con la lunghezza d’onda delle onde.

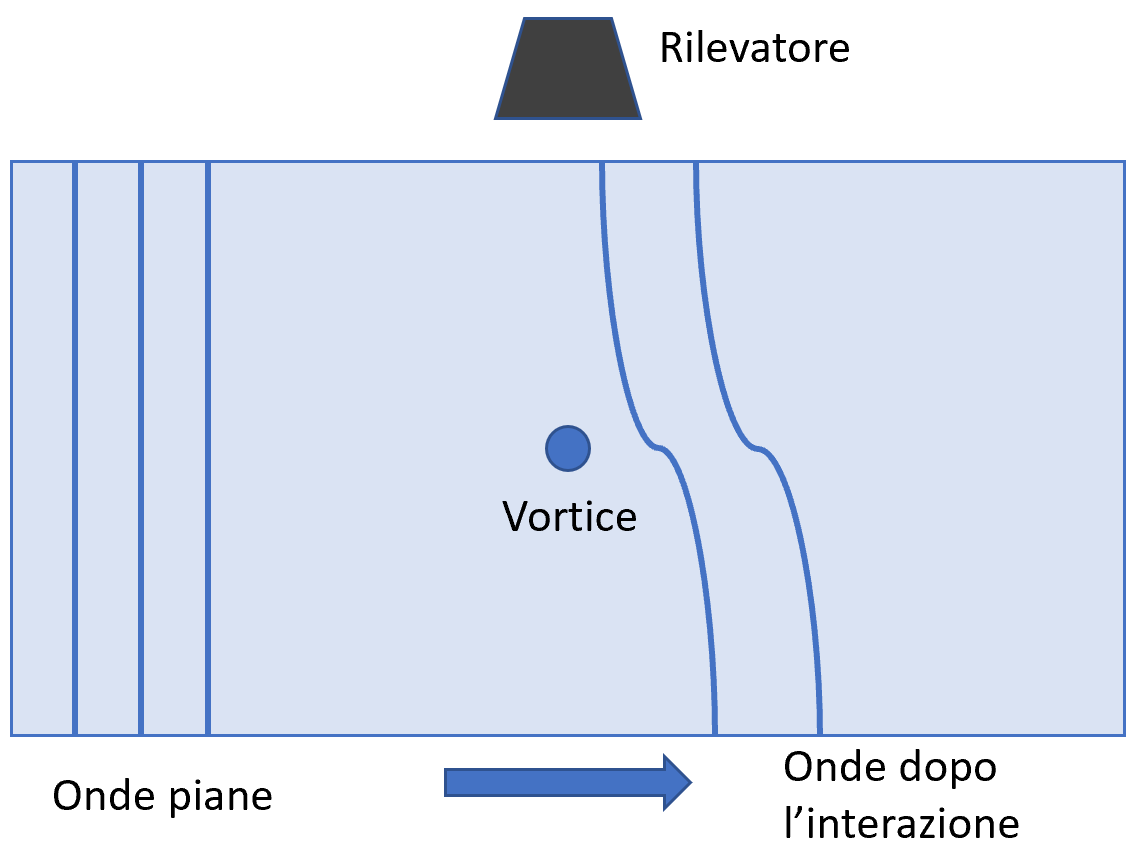
Schema del setup sperimentale: le onde piane si muovono da destra verso sinistra e interagiscono con il vortice, posto al centro della vasca. Da qui proseguono il loro percorso fino a terminare la corsa sull’altro bordo. Il processo viene registrato da due telecamere che permettono poi di poter analizzare il processo.

I dati ottenuti sono poi analizzati scomponendo le onde piane nelle componenti azimutali, che sono quelle che ci interessano per studiare come i vari modi positivi (corotanti) e negativi (controrotanti) interagiscano con il vortice. Dalla ricostruzione i ricercatori sono stati in grado di notare come i modi che sono corotanti con il vortice (e che quindi soddisfano le condizioni per la superradianza) vengono amplificati, sottraendo energia al vortice in un processo analogo a quello di superradianza teorizzato per i buchi neri.

Conclusione

L’esperimento realizzato permette dunque di avere un’idea qualitativa di quello che potrebbe succedere in un intorno del buco nero. Questo richiede la preparazione di un sistema che presenti delle proprietà simili, in modo da poter paragonare quello che succede in laboratorio con le teorie.

Come già accennato nell’introduzione, l’approccio analogo ha altre implementazioni oltre a quella approfondita in questo articolo. In particolare i modelli analoghi sono studiati nei sistemi di gas ultrafreddi, con i condensati di Bose-Einstein, perché sono sistemi più controllabili e di cui si ha una conoscenza più ampia. Diversamente, sistemi realizzati con l’acqua, la fluidodinamica è molto complessa e sono meno adatti a certi utilizzi.

Lo studio degli analoghi è diffuso in diversi centri di ricerca in quanto riunisce gli interessi di molti campi diversi, dalla fisica dello stato solido e degli atomi ultrafreddi fino alla relatività generale e alla fisica delle alte energie. L’Università di Trento collabora attivamente a questo filone di ricerca concentrando i suoi sforzi nello studio di sistemi di condensato di Bose-Einstein: all’interno di questi studi, negli scorsi anni, alcuni ricercatori hanno dato un contributo importante sviluppando un modo per misurare la radiazione di Hawking. Tale attività di ricerca è svolta in cooperazione con il BEC Center, centro di ricerca in collaborazione tra l’INO-CNR e il Dipartimento di Fisica dell’Università di Trento.

Contatti utili

Alessio Recati

Iacopo Carusotto

“Gravità Analoga” di Alberto Canali, Associazione Italiana Studenti di Fisica, è distribuito con Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale.