Il protone intelligente

Come l’uso di reti neurali e di algoritmi genetici ha rivoluzionato lo studio delle Parton Distribution Functions (PDFs) del protone.

(A cura di Giovanni Stagnitto, Università degli Studi di Milano)

Dopo la meritata euforia “domenicale” seguita alla scoperta del bosone di Higgs, negli ultimi anni il mondo della fisica delle particelle sta vivendo un travagliato “lunedì”: i tanto bramati indizi di nuova fisica oltre il Modello Standard delle interazioni fondamentali tardano ad arrivare. In attesa di aumentare l’energia del Large Hadron Collider (LHC) per esplorare nuovi regimi cinematici e quindi permettere la produzione di eventuali nuove particelle, l’obiettivo è mettere alla prova sempre di più le predizioni del Modello Standard, grazie a misure più accurate o di piccole deviazioni dei dati rispetto alle previsioni teoriche, alla ricerca di ulteriori conferme sperimentali. Precisione e accuratezza sono pertanto le parole chiave che guidano il lavoro di fisici teorici e sperimentali in questo decennio. Per un acceleratore di protoni e ioni come LHC la Quantum Chromodynamics (QCD), quella parte di Modello Standard che descrive le interazioni forti, è di fondamentale importanza.

• live_help Il modello a quark

  Il protone non è una particella elementare, come per esempio l’elettrone o il muone. La sua struttura interna è molto complessa, anche se ad energie ordinarie buona parte delle sue proprietà possono essere spiegate assumendo che sia costituito da due quark up (con carica +⅔) e un quark down (con carica -⅓), e questi quark siano legati tra loro dai mediatori della forza forte, i cosiddetti gluoni. La loro presenza è necessaria anche per giustificare la massa del protone, ordini di grandezza maggiore della somma delle masse dei quark up e down: infatti la massa del protone è data per il 99.9% dall’energia di legame tra i costituenti. Nel Modello Standard esistono 6 tipologie di quark, ognuno con un'etichetta (detta flavour) diversa: oltre ai quark up (u) e down (d), esistono anche il quark strange (s), charm (c), bottom (b) e top (t).

All’interno della fisica di LHC, un ruolo particolare è svolto dalle cosiddette distribuzioni di struttura partonica del protone, in inglese Parton Distribution Functions (PDFs), che sono l’oggetto di questo articolo. Per capire come esse entrino in gioco, occorre fare una breve digressione sul concetto che sta alla base delle predizioni di QCD per i processi di LHC, ovvero la cosiddetta fattorizzazione, che può essere compresa grazie all’aiuto della Figura 1, in cui è schematizzato lo scattering di due protoni A e B.

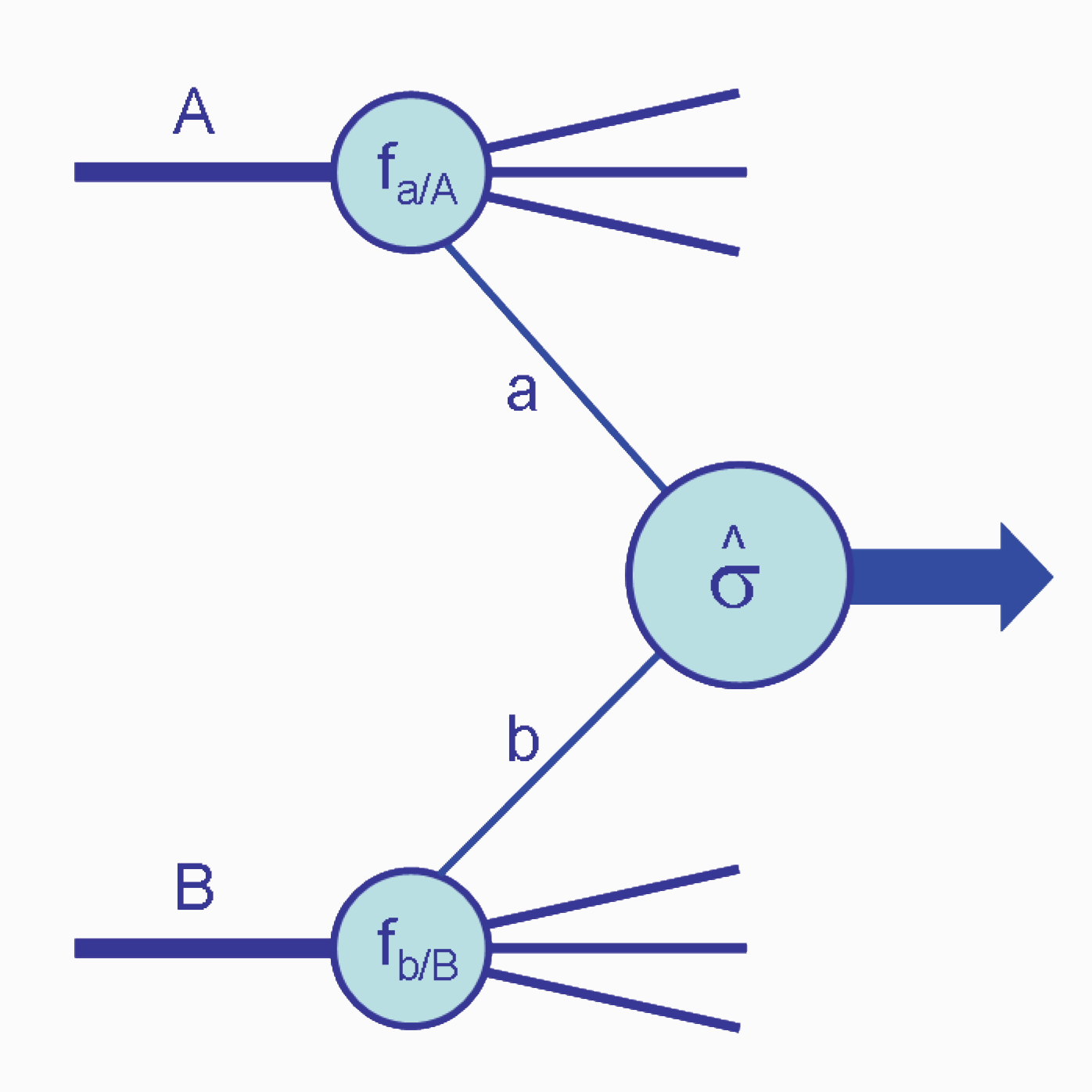
Figura 1: Rappresentazione schematica della fattorizzazione [1].

L’alta energia di LHC agisce come una “lente di ingrandimento” dotata di grande risoluzione e ci permette di osservare direttamente i costituenti interni del protone, i cosiddetti partoni (quark e gluoni): l’etichetta a (b) in Figura 1 indica proprio questo. Si può dire, quindi, che il processo avviene non direttamente tra i protoni, ma tra i partoni che, estratti dal grembo protonico materno con una certa frazione $x$ di quantità di moto (o più semplicemente, in un determinato limite, una frazione $x$ della massa del protone), interagiscono dando luogo a stati finali rivelati dai detector che circondano la linea del fascio. I partoni sono confinati ovvero non possono esistere liberi e dopo il processo d’urto si ricombinano sempre per formare nucleoni, come il protone o il neutrone, o altri tipi di particelle composite. Il confinamento è il motivo per cui la fattorizzazione si rende necessaria. Essa consiste consiste nell’affermare che il calcolo del processo possa venire fattorizzato in due contributi:

Il fattore a destra indica il processo di interazione tra partoni e può essere calcolato da principi primi in modo perturbativo: si espande la sezione d’urto in una serie di potenze nella costante $\alpha_s$, che rappresenta l’intensità del legame tra partoni e diminuisce sempre più al crescere dell’energia (libertà asintotica), e di questa serie si possono considerare solo i primi termini. Il fattore a sinistra invece codifica tutta la dinamica non perturbativa delle basse energie: l’espansione in serie prima citata non è più possibile. A tutti gli effetti una mistery box, che racchiude in sé la risposta alla domanda “Quale è la probabilità di estrarre dal grembo di mamma protone un quark di un determinato flavour a (b) che porti una certa frazione $x_{1} (x_{2})$ di quantità di moto del protone?”. Questo oggetto si chiama Parton Distribution Function (PDF).

Esse sono state a lungo studiate dal punto di vista teorico ed è noto che dipendono da due variabili, ovvero dall’energia Q² con cui viene sondato il protone (la quale può essere considerata come detto prima il grado di “risoluzione” della nostra lente) e dalla frazione $x$ di quantità di moto (o anche momento nel seguito) con cui il partone di un generico flavour f viene estratto dal protone. Mentre la dipendenza delle PDFs da $x$ può essere ricavata solo dai dati sperimentali, la dipendenza da Q² è descritta dalle equazioni di Alterelli e Parisi (o anche DGLAP), un grande successo della QCD perturbativa (l’articolo di Altarelli e Parisi è uno degli articoli più citati di tutti i tempi) [2]. Tuttavia, per poter risolvere le DGLAP è necessario conoscere le condizioni iniziali, che devono essere anch’esse ricavate dai dati sperimentali (a causa del carattere non perturbativo della dinamica).

Osservando la Figura 2, nella quale è rappresentata la dipendenza delle PDFs da $x$ (notare la scala logaritmica) per due scale di energia diverse (a sinistra una scala “bassa” mentre a destra una scala “alta” tipica di LHC), possiamo fare qualche considerazione qualitativa sulla struttura interna del protone. Per alti valori di $x$ (grandi frazioni di momento) troviamo due picchi corrispondenti ai quark up e al quark down, con circa un rapporto 2:1, mentre gli altri flavour sono praticamente assenti: per questo motivo si dice che il protone sia composto da due quark up e da un quark down. Al diminuire di $x$ (quindi per frazioni di momento via via minori), comincia a crescere anche il contributo di quark anche di flavour diverso da u e d, generati a coppie secondo il processo di splitting $g\rightarrow quark+antiquark$. Leader indiscusso per bassi valori di $x$ è però il gluone (notare il fattore 1/10) e tale caratteristica si accentua ancora di più con il crescere della scala Q².

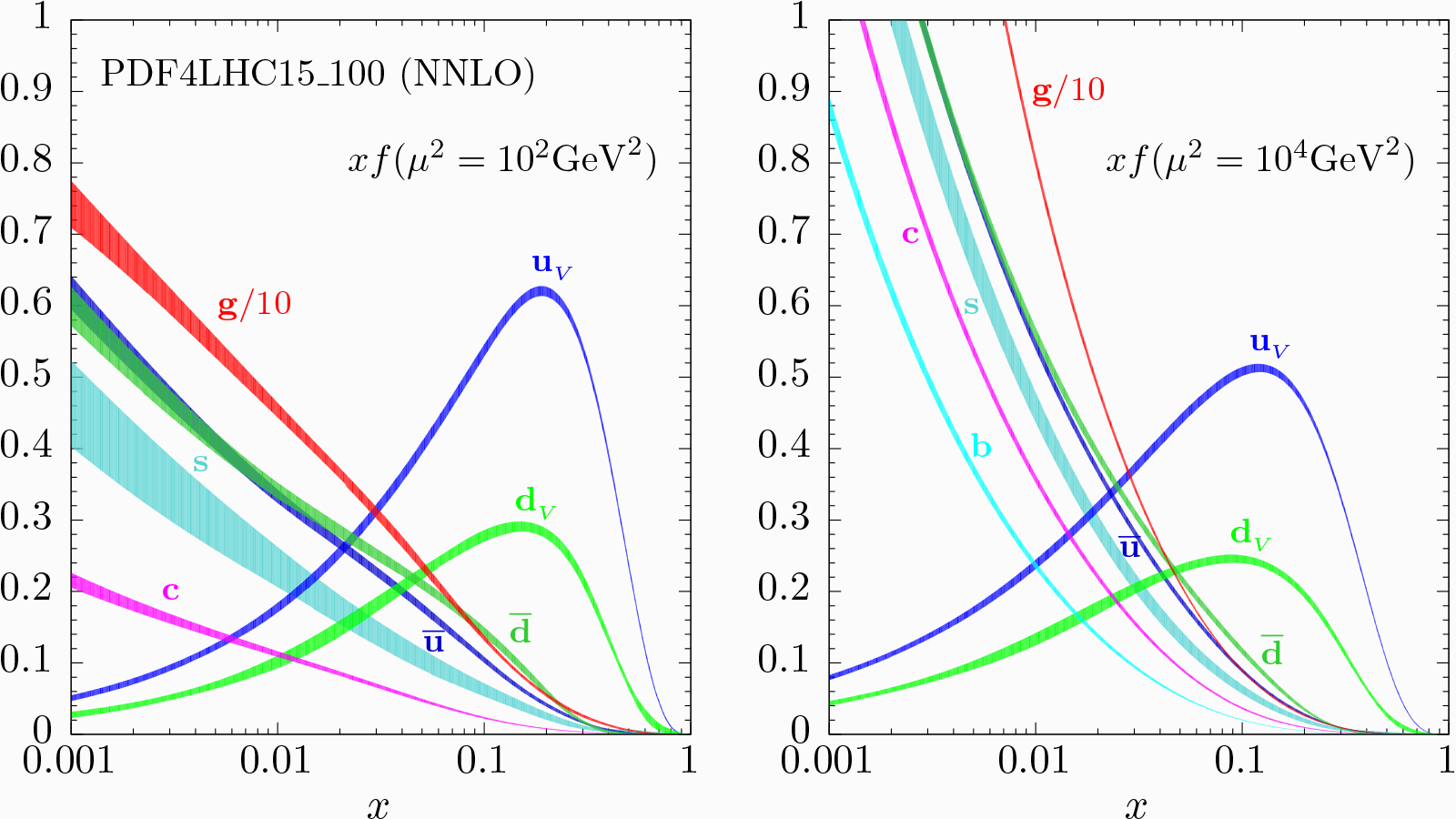
Figura 2: Dipendenza delle PDFs da $x$ (notare la scala logaritmica) per due scale di energia diverse (a sinistra una scala “bassa” mentre a destra una scala “alta” tipica di LHC) [3].

Come si determinano le PDFs?

Il problema principale dietro alla determinazione delle PDFs sta nella loro forma funzionale (cioè che aspetto abbiano le funzioni $f_{q,g}(x)$): nessuno sa quale sia la forma corretta, vi sono solo alcune identità formali, dovute a considerazioni teoriche, che esse devono rispettare. Il metodo standard prevede la scelta di una base di funzioni specifica (spesso potenze di x i cui esponenti vengono lasciati come parametri) e il confronto con il dato sperimentale permette di risalire al valore dei parametri ignoti presenti Una volta ottenuta una stima dell’andamento delle PDFs, è opportuno come in ogni buona predizione fisica quantificare la nostra incertezza, andando a stabilire opportuni intervalli di confidenza. L’assunzione di una particolare parametrizzazione forza il sistema a convergere in una determinata direzione, escludendo di fatto altre possibili forme funzionali. Ciò comporta uno sottostima delle incertezze e accade che, cambiando forma funzionale di partenza o determinando i parametri usando sottoinsiemi diversi dei dati sperimentali a disposizione, il risultato finale per l’andamento delle PDFs sia ben al di fuori dell’intervallo di confidenza stimato (ovvero la probabilità che questo accada è maggiore dei livelli di confidenza associati agli intervalli).

Un metodo alternativo per la determinazione delle PDFs è stato introdotto dalla collaborazione NNPDF (Neural Networks PDF) nello scorso decennio, e prevede l’uso massiccio di tecniche di intelligenza artificiale. La collaborazione, guidata dal prof. Stefano Forte dell’Università degli Studi di Milano, conta attualmente 15 membri di 12 diverse istituzioni in 5 stati europei e fornisce periodicamente alla comunità scientifica set aggiornati di PDFs, includendo gradualmente i nuovi dati sperimentali e migliorando il metodo di analisi (l’ultima versione 3.1 è del giugno 2017). L’importanza di aggiungere sempre più rilevazioni sperimentali sta nel fatto che ogni particolare osservabile permette di esplorare zone diverse del piano Q²-$x$ (vedi Figura 3) e soprattutto alcune osservabili sono più sensibili a determinate PDFs rispetto ad altre.

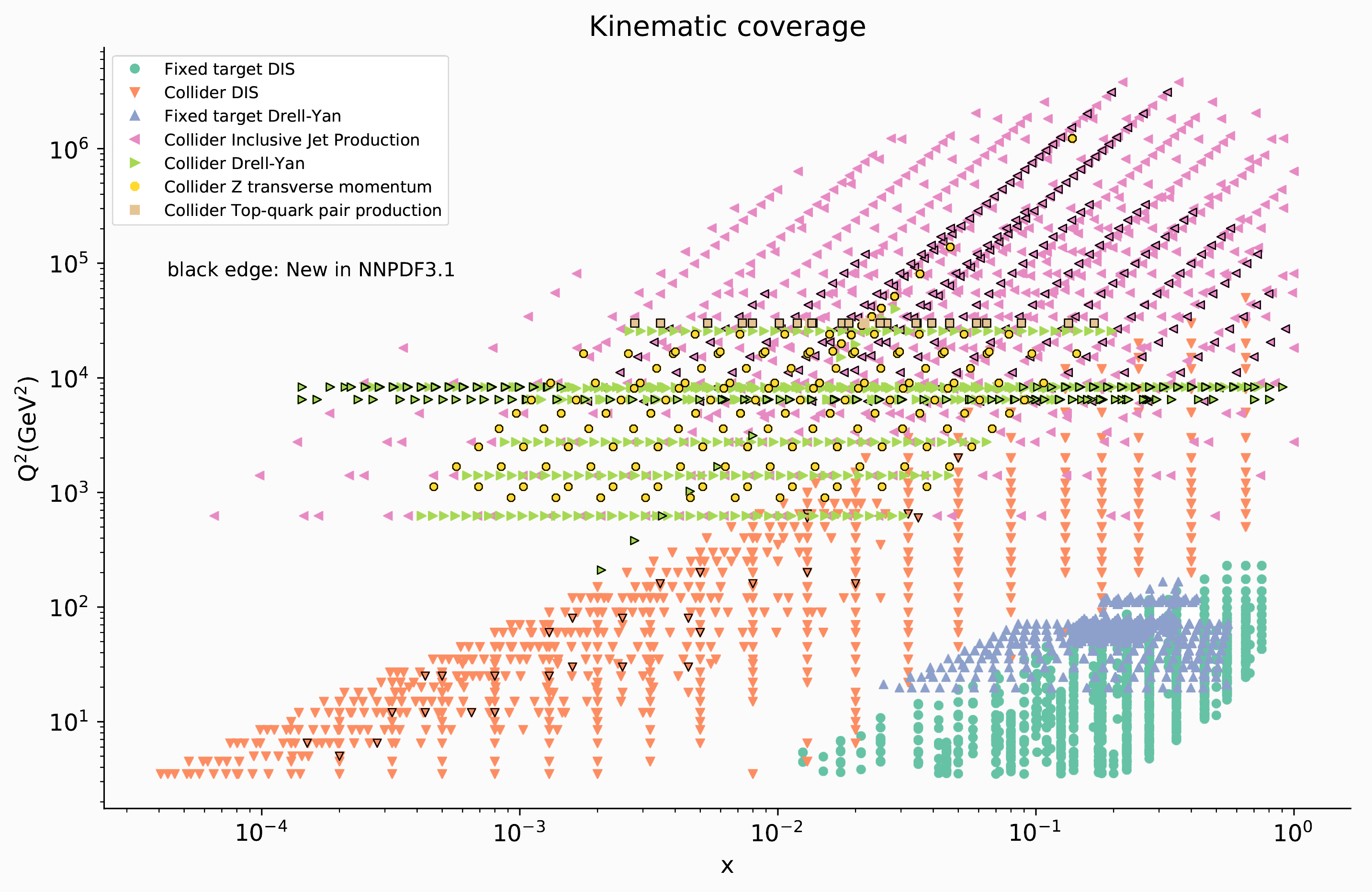
Figura 3: Disposizione dei dati sperimentali utilizzati nei fit di PDF all’interno del piano $x$ - Q² [3].

Da questo punto fino al termine dell’articolo, tenteremo di spiegare con parole semplici come funzionano le tecniche di machine learning adottate dalla collaborazione. Partiamo dai dati: assumiamo che ogni dato rappresenti il valore medio di una distribuzione di probabilità e che la deviazione standard sperimentale rappresenti la larghezza di tale distribuzione. Usando la distribuzione di probabilità così costruita, generiamo casualemente dati sperimentali facsimile in modo che i parametri medi di questo campione, all’aumentare della numerosità del campione, tendano ai valori veri (metodi di questo tipo basati sulla generazione casuale di eventi prendono il nome di simulazioni Monte Carlo, in onore del celebre porto mediterraneo patria dei casinò).

A questo punto occorre parametrizzare opportunamente le PDFs. Per fare questo, la collaborazione NNPDF si appoggia sull’utilizzo di una rete neurale. La rete neurale è un interpolante universale: ciò significa che essa è in grado di riprodurre qualsiasi forma funzionale usando un numero finito di parametri. Nel nostro caso, la rete neurale modellizza la mistery box di cui abbiamo parlato prima, la quale collega a fissato input ($x$) un fissato output (i punti sperimentali sotto forma di repliche alla Monte Carlo). L’idea è quella di simulare un passaggio di informazioni tra “neuroni” interconnessi mediante “sinapsi” di collegamento. Ogni neurone è caratterizzato da un parametro $\xi_i$, mentre la sinapsi che connette i neuroni i e j è caratterizzata da un peso $\omega_{ij}$. Lo stato $\xi_i$ è una funzione $g$ dei pesi $\omega_{ij}$ delle sinapsi che lo raggiungono, degli stati nei neuroni circostanti $\xi_j$ e di una soglia $\theta_i$ che sta a indicare l’attivazione o meno del neurone:

Affinchè la rete neurale funzioni, la funzione $g$ di attivazione deve comprendere zone di andamento non lineare. Un esempio di funzione $g$ di solito usata nelle reti neurali è rappresentata nella Figura 4.

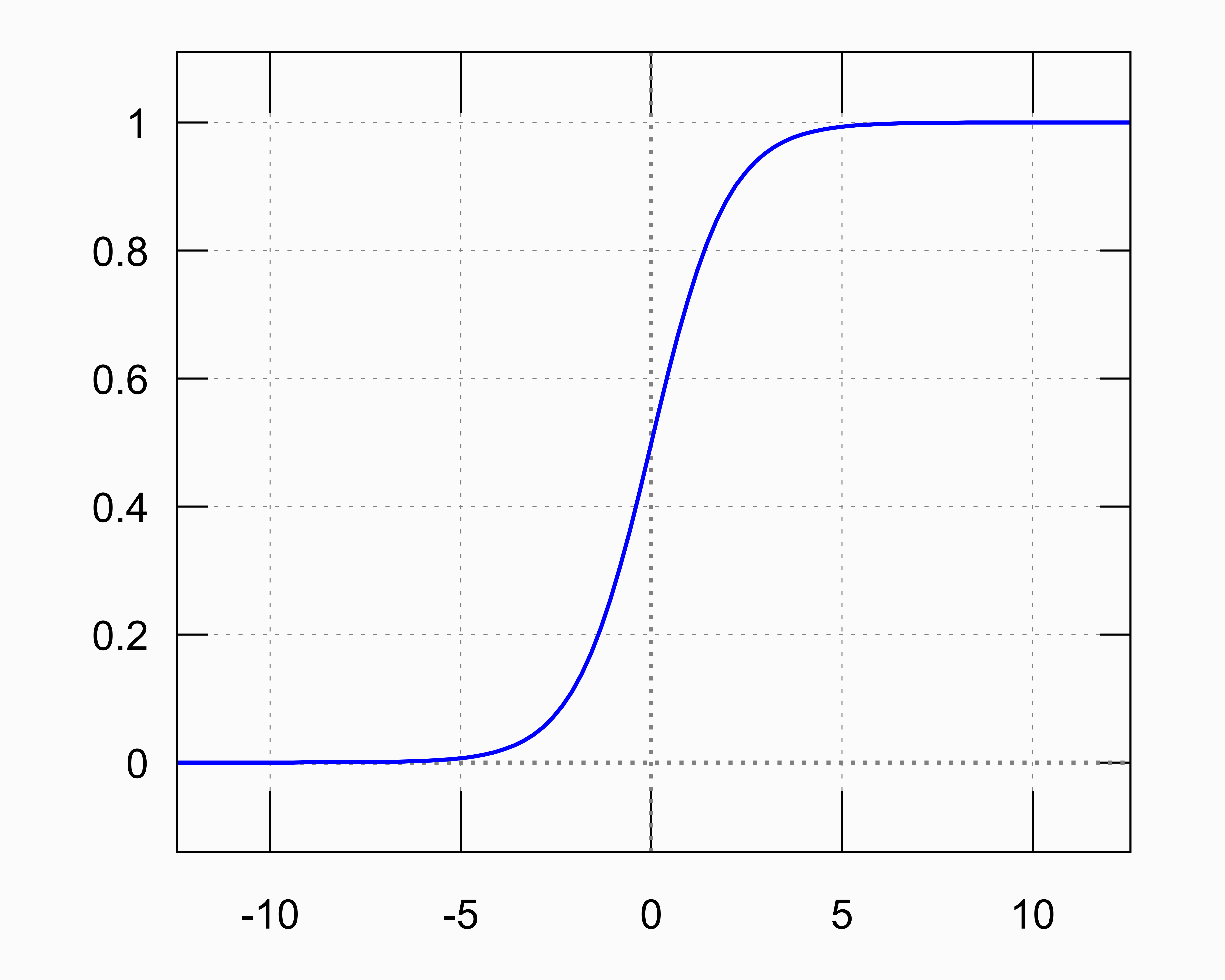
Figura 4: Tipica funzione di attivazione usata nelle reti neurali: $g(z) = \frac{1}{1+e^{-z}}$.

Essa è caratterizzata da una risposta lineare nei dintorni di $z\sim 0$ e satura per grandi valori negativi e positivi di $z$, con un’opportuna taratura dei pesi e delle soglie, si può fare in modo che essa lavori nelle zone di transizione tra il regime lineare e di saturazione, e che quindi possa riprodurre andamenti anche non banali. Grazie a questo meccanismo, ogni funzione continua può essere modellizzata mediante una rete neurale.

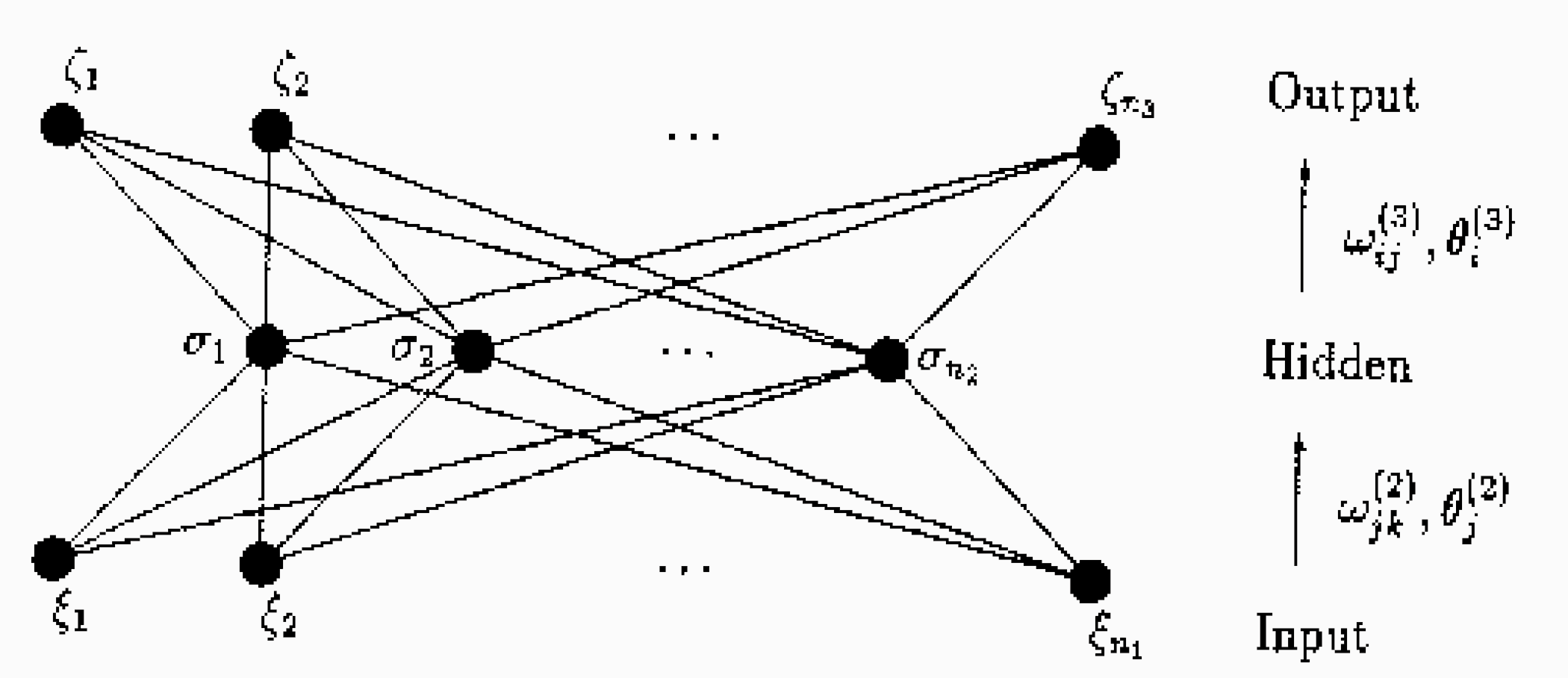
Figura 5: Esempio di topologia tipica di rete neurale, organizzata su 3 layer: input - hidden - output [4].

Una volta compreso il meccanismo di funzionamento, occorre trovare i giusti valori dei parametri $\xi$ e $\omega$ per descrivere la funzione che, partendo dall’input introdotto, restituisca l’output desiderato. Ciò può essere fatto iterativamente. Innanzitutto viene definito un funzionale da minimizzare che esprime la deviazione tra l’output della rete e l’output richiesto. La minimizazione di tale funzionale viene implementata operativamente tramite l’adozione di un algoritmo genetico. L’idea è quella di riprodurre un processo di selezione naturale simile a quello darwiniano: viene generato in modo casuale un gran numero di possibili configurazioni di parametri della rete e vengono scelte solo le configurazioni più adatte o incroci delle configurazioni più adatte. Partendo da queste e introducendo delle mutazioni, il processo viene iterato per un ottimale numero di iterazioni.

Parliamo di valore “ottimale” perchè il rischio nel tenere accesa troppo a lungo la macchina neurale è quello di un apprendimento eccessivo che giunga a cogliere il rumore statistico presente nell’insieme dei dati. Ricordiamo che in virtù del suo essere un interpolante universale, la rete neurale può riprodurre qualsiasi funzione continua, cosa che non può accadere nel caso in cui la funzione sia espressa in termini di base di funzioni fissata. Pertanto il rischio dietro all’uso di una rete neurale è quello di perdere il controllo sulla procedura di interpolazione. Visivamente si può cogliere questo fatto nella Figura 6, nella quale i punti vuoti con la barra di errore rappresentano i dati sperimentali, mentre i punti pieni sono l’output della rete neurale dopo un diverso numero di iterazioni di apprendimento: poche iterazioni (sotto-apprendimento), il “giusto” numero (apprendimento ideale), eccessive iterazioni (sovra-apprendimento).

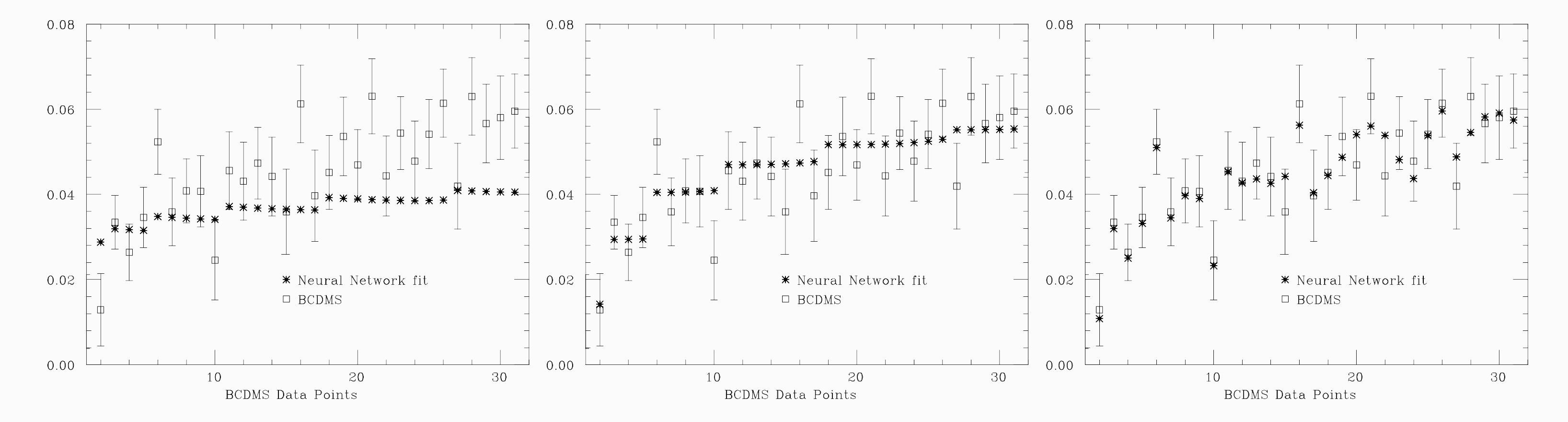
Figura 6: Risultato dell’output della rete neurale dopo un numero diverso di iterazioni (vedi testo) [4].

L’affermazione riguardo al fatto che quello sia il “giusto” numero nasce dall’occhio dell’uomo che “vede” una ragionevole curva liscia seguire l’andamento dei punti sperimentali, ma come può una macchina scegliere quando fermarsi? Un criterio oggettivo è quello del cross-validation: i punti sperimentali vengono suddivisi arbitrariamente in due gruppi, un gruppo di apprendimento e uno di validazione, ma solo i punti del gruppo di apprendimento vengono considerati ai fini del fitting; ovvero in altre parole si minimizza solo il $\chi^2$ di apprendimento, monitorando però allo stesso tempo anche il $\chi^2$ di validazione. Ebbene, il punto di apprendimento ideale è definito come il numero di iterazioni in corrispondenza del quale il $\chi^2$ di validazione smette di diminuire, a differenza di quello di apprendimento. Nella Figura 7 è mostrato un esempio esplicito della procedura: a sinistra si vede chiaramente come in questo caso il numero di iterazioni ideale si assesti intorno a 2000 (tale numero varia molto da replica a replica).

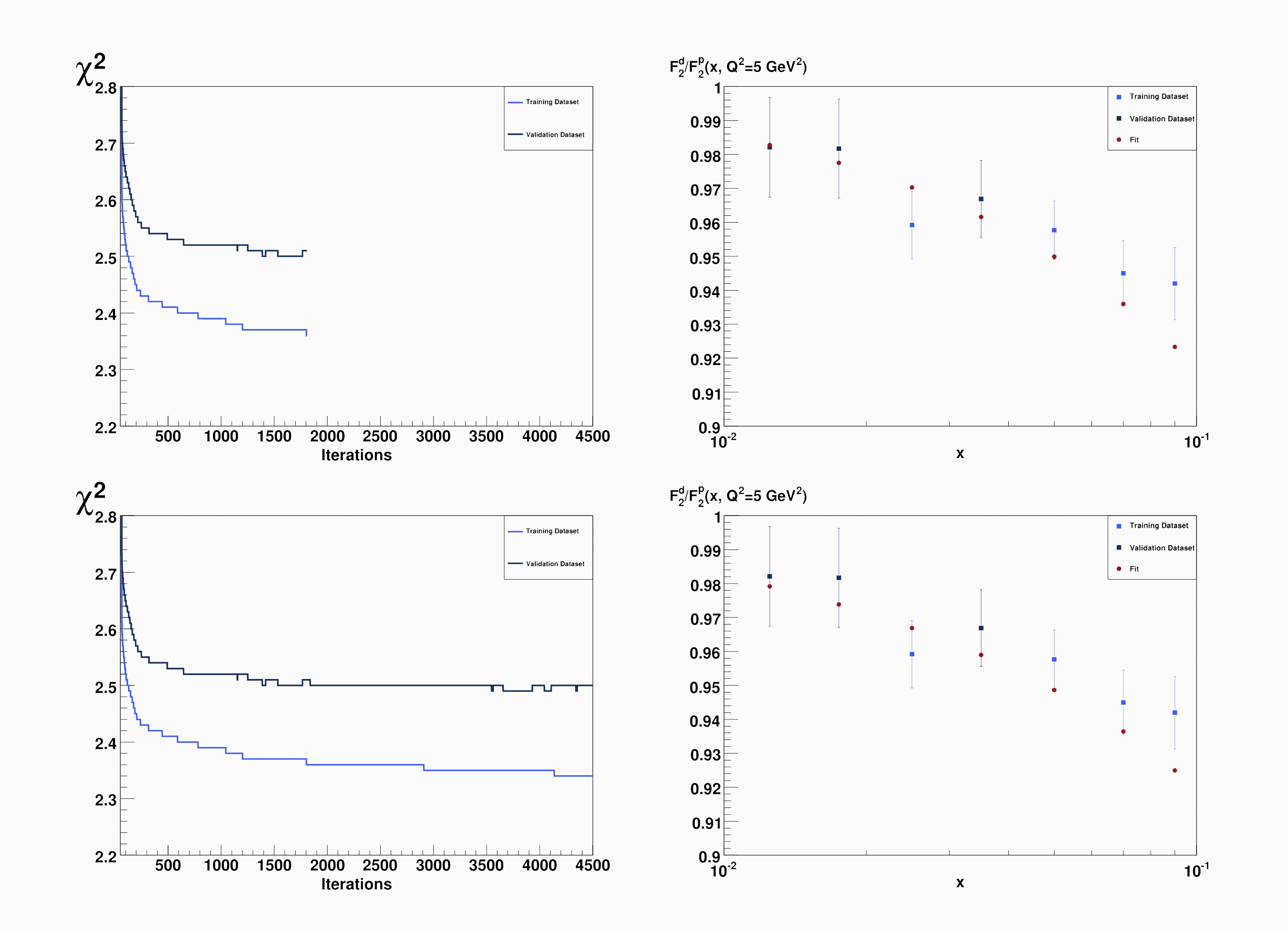
Figura 7: Metodo cross-validation per stabilire il corretto numero di iterazioni della rete neurale [5].

Una volta terminata l’iterazione della rete neurale per ogni replica Monte Carlo dei dati sperimentali, abbiamo a disposizione un set di repliche di PDF e otteniamo la PDF ricercata come media di questo set. Ma non solo: uno dei grandi vantaggi del metodo NNPDF è quello di fornire allo stesso tempo anche intervalli di incertezza affidabili, nel senso che le incertezze possono essere interpretate in senso statistico stretto. In termini frequentisti questo per esempio significa che, andando a considerare l’intervallo di confidenza a $1\sigma$ ($\approx 68\%$) attorno al valore centrale, esso conterrà un numero di repliche pari circa a 68. Tale comportamento è rappresentato nella Figura 8 per la PDF del gluone.

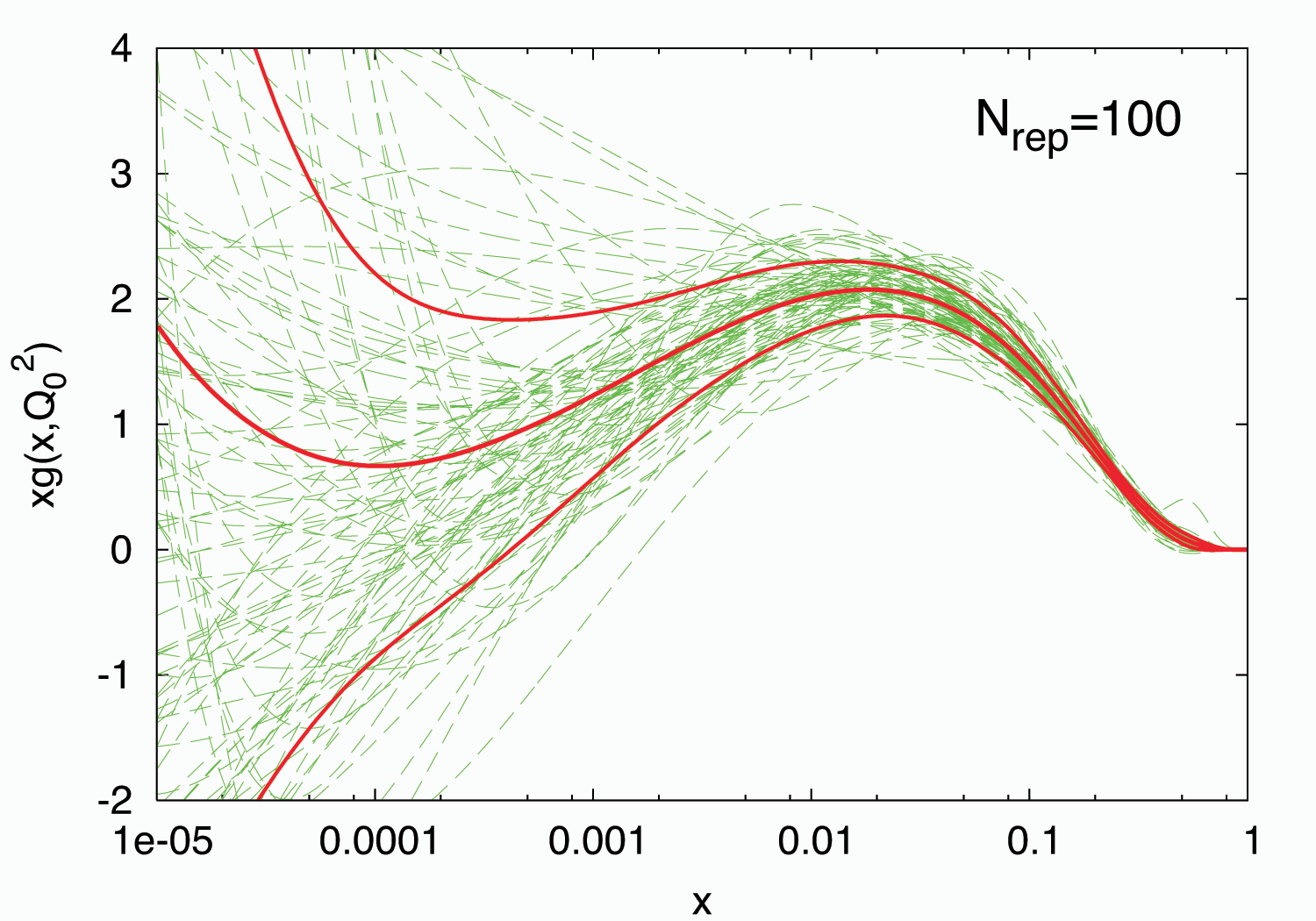
Figura 8: 100 repliche della PDF del gluone (linee verdi), con loro valore centrale e intervallo $1\sigma$ attorno al valore centrale (linee rosse) [5].

Riassumendo, il metodo basato sull’uso di reti neurali ha provocato una piccola rivoluzione in questo campo affascinante e di grande importanza per la fisica delle alte energie dei prossimi anni. Il prof. Forte ha recentemente vinto un Advanced Grant bandito dall’European Research Council, grazie al quale sarà portato avanti lo studio di tecniche di intelligenza artificiale per le PDFs, con l’introduzione di reti neurali più profonde e complesse. Il progetto è chiamato N3PDF e sono attualmente aperte due posizioni (con scadenza il 1 aprile) per studenti che cominceranno il dottorato il prossimo anno (https://academicjobsonline.org/ajo/jobs/10735). Se avete trovato interessati gli argomenti trattati in questo articolo, perchè non fare domanda?

Per approfondire

[1] J. M. Campbell, J. W. Huston, W. J. Stirling. “Hard Interactions of Quarks and Gluons: A Primer for LHC Physics”.

[2] G. Altarelli, G. Parisi. “Asymptotic freedom in parton language”. Nucl. Phys. B, 126 (1977).

[3] J. Gao, L. Harland-Lang, J. Rojo. “The Structure of the Proton in the LHC Precision Era”.

[4] S. Forte, L. Garrido, J.I. Latorre, A. Piccione. “Neural network parametrization of deep inelastic structure functions”.

[5] S. Forte. “Parton distributions at the dawn of the LHC”.

[6] NNPDF Collaboration. “A Determination of parton distributions with faithful uncertainty estimation”.

Contatti utili

Prof. Stefano Forte

“Il protone intelligente” di Giovanni Stagnitto, Associazione Italiana Studenti di Fisica, è distribuito con Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale.